If you used computer simulations to make all the correct decisions in 2 deck blackjack (all the correct decisions would obviously be based on what's left in the shoe, because computers can keep track of 13 counts.. penetration almost all the way to the end of the second shoe every time. What kind of advantages would this computer simulation present? 54%? 55%?
2 deck, perfect play blackjack
- Thread starter guitarhero
- Start date
guitarhero said:
If you used computer simulations to make all the correct decisions in 2 deck blackjack (all the correct decisions would obviously be based on what's left in the shoe, because computers can keep track of 13 counts.. penetration almost all the way to the end of the second shoe every time. What kind of advantages would this computer simulation present? 54%? 55%?
Imagine we were down to the last ten cards in the shoe and there were 6 high cards and 4 low cards remaining, your advantage would be quite high at the end. If there were 10 cards remaining and the computer knew that 6 were tens, and the low cards were 8, 6, 5, 3, it would be easy for the computer to calculate all the possible hands and the correct odds for each. You would have a 60% chance of catching a ten on your first card, and a 56% chance of catching another ten on your second card, for a 34% chance of making a twenty. Of course, the dealer has the same chance, plus the fact that the dealer may also make a perfect hand in two ways, ten/8/3 and ten/6/5, not that these are not also available to you.
Some cases would be way lopsided in your favor, such as when there are five aces and 5 tens remaining. Chances are you will not be unfortunate enough to split aces and receive hits of two aces. :laugh: BTW, if you get two tens, and the dealer has a ten showing, it would be a good time to split tens, and keep splitting them until you no longer can, since only twenty-one can win that hand. :laugh:
I have no idea what the simulation would show overall, but it should be pretty healthy.
Would like some advice on 2 deck games!I never heard of a book talking about 2 deck games in depth.Since playing decision is so important and it is only single deck that get all the attention .I think 2deck games sort of got stuck in the middle between sd and 6 decks.There is not a lot of info that help us to play the game.The playing decision of 16 vs 10 and 15 vs 10 ,3 card 16 vs 9 ,15 vs 9 are so important .Just relying on basic strategy does not seem to be enough even with the help of index play with hi lo (since thats what i use)How many 4,5 needs to be played out or not play out to change a decision of hit/stand? Would the "Theory of Blackjack" help me to make a few adjustment for my use with the understanding of E.O.R. for 4,5 maybe ??Is there a more accurate way of playing insurance rather than just using hi lo 's insurance index of 2.4 in 2 deck/,but without going to "ten count" or "VIP COUNT" for insurance. I am obviously quite confuse of what to do in 2 deck since there is not a lot of info on it!I better stop typing because i m more lost than i was originally!!!!
guitarhero said:
If you used computer simulations to make all the correct decisions in 2 deck blackjack (all the correct decisions would obviously be based on what's left in the shoe, because computers can keep track of 13 counts.. penetration almost all the way to the end of the second shoe every time. What kind of advantages would this computer simulation present? 54%? 55%?
guitarhero said:
If you used computer simulations to make all the correct decisions in 2 deck blackjack (all the correct decisions would obviously be based on what's left in the shoe, because computers can keep track of 13 counts.. penetration almost all the way to the end of the second shoe every time. What kind of advantages would this computer simulation present? 54%? 55%?
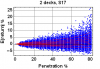
The plot is a combination of simulation and combinatorial analysis: the blue points result from simulation of heads-up play through 1000 shuffled shoes; each point is the expected return for a corresponding depleted shoe, assuming "perfect" play optimized for that depleted shoe. The red curves are 10, 20, 30, ..., 90th percentile curves of the blue points. So, for example, even at 80% penetration (only about 20 cards left), 90% of the time your EV is less than 9%.
Hope this helps,
Eric
Attachments
-
10.4 KB Views: 1,162
ericfarmer said:
Usually no more than 5-10%, but possibly as much as 25%. The attached plot shows the distribution of expected return (in % of initial wager) vs. penetration (in % of the 104 cards in the shoe), assuming CDZ- strategy with ridiculously optimistic rules: S17, DOA, SPL4, RSA, with surrender.
The plot is a combination of simulation and combinatorial analysis: the blue points result from simulation of heads-up play through 1000 shuffled shoes; each point is the expected return for a corresponding depleted shoe, assuming "perfect" play optimized for that depleted shoe. The red curves are 10, 20, 30, ..., 90th percentile curves of the blue points. So, for example, even at 80% penetration (only about 20 cards left), 90% of the time your EV is less than 9%.
Hope this helps,
Eric
The plot is a combination of simulation and combinatorial analysis: the blue points result from simulation of heads-up play through 1000 shuffled shoes; each point is the expected return for a corresponding depleted shoe, assuming "perfect" play optimized for that depleted shoe. The red curves are 10, 20, 30, ..., 90th percentile curves of the blue points. So, for example, even at 80% penetration (only about 20 cards left), 90% of the time your EV is less than 9%.
Hope this helps,
Eric
ericfarmer said:
Usually no more than 5-10%, but possibly as much as 25%. The attached plot shows the distribution of expected return (in % of initial wager) vs. penetration (in % of the 104 cards in the shoe), assuming CDZ- strategy with ridiculously optimistic rules: S17, DOA, SPL4, RSA, with surrender.
The plot is a combination of simulation and combinatorial analysis: the blue points result from simulation of heads-up play through 1000 shuffled shoes; each point is the expected return for a corresponding depleted shoe, assuming "perfect" play optimized for that depleted shoe. The red curves are 10, 20, 30, ..., 90th percentile curves of the blue points. So, for example, even at 80% penetration (only about 20 cards left), 90% of the time your EV is less than 9%.
Hope this helps,
Eric
The plot is a combination of simulation and combinatorial analysis: the blue points result from simulation of heads-up play through 1000 shuffled shoes; each point is the expected return for a corresponding depleted shoe, assuming "perfect" play optimized for that depleted shoe. The red curves are 10, 20, 30, ..., 90th percentile curves of the blue points. So, for example, even at 80% penetration (only about 20 cards left), 90% of the time your EV is less than 9%.
Hope this helps,
Eric
MountainMan said:
What software was used to generate the grafic?
ericfarmer said:
Usually no more than 5-10%, but possibly as much as 25%. The attached plot shows the distribution of expected return (in % of initial wager) vs. penetration (in % of the 104 cards in the shoe), assuming CDZ- strategy with ridiculously optimistic rules: S17, DOA, SPL4, RSA, with surrender.

The plot is a combination of simulation and combinatorial analysis: the blue points result from simulation of heads-up play through 1000 shuffled shoes; each point is the expected return for a corresponding depleted shoe, assuming "perfect" play optimized for that depleted shoe. The red curves are 10, 20, 30, ..., 90th percentile curves of the blue points. So, for example, even at 80% penetration (only about 20 cards left), 90% of the time your EV is less than 9%.
The plot is a combination of simulation and combinatorial analysis: the blue points result from simulation of heads-up play through 1000 shuffled shoes; each point is the expected return for a corresponding depleted shoe, assuming "perfect" play optimized for that depleted shoe. The red curves are 10, 20, 30, ..., 90th percentile curves of the blue points. So, for example, even at 80% penetration (only about 20 cards left), 90% of the time your EV is less than 9%.
zengrifter said:
well, i stand corrected! Zg
Attachments
-
1.8 KB Views: 460
ericfarmer said:
Usually no more than 5-10%, but possibly as much as 25%. The attached plot shows the distribution of expected return (in % of initial wager) vs. penetration (in % of the 104 cards in the shoe), assuming CDZ- strategy with ridiculously optimistic rules: S17, DOA, SPL4, RSA, with surrender.
The plot is a combination of simulation and combinatorial analysis: the blue points result from simulation of heads-up play through 1000 shuffled shoes; each point is the expected return for a corresponding depleted shoe, assuming "perfect" play optimized for that depleted shoe. The red curves are 10, 20, 30, ..., 90th percentile curves of the blue points. So, for example, even at 80% penetration (only about 20 cards left), 90% of the time your EV is less than 9%.
Hope this helps,
Eric
The plot is a combination of simulation and combinatorial analysis: the blue points result from simulation of heads-up play through 1000 shuffled shoes; each point is the expected return for a corresponding depleted shoe, assuming "perfect" play optimized for that depleted shoe. The red curves are 10, 20, 30, ..., 90th percentile curves of the blue points. So, for example, even at 80% penetration (only about 20 cards left), 90% of the time your EV is less than 9%.
Hope this helps,
Eric
The long term data would start with the same expected value which is full shoe EV at 0 cards pen. The short term data for 0 cards pen would be dependent on what actually happened on the first hand of the simmed shoe.
As an arbitrary example let's look at what might be plotted for 75 cards pen. Out of 1000 shoes simmed not every shoe would wind up with exactly 75 cards dealt for the next deal but probably at least some of them would. So the long term point for 75 cards would be the average pre-deal EV of the hands where exactly 75 cards have been dealt and the short term point would be the computed EV of the actual results of playing the simulated hands according to the best decision.
One thing to look out for is to choose a max pen so as not to ever run out of cards to keep from incorporating unreliable data.
I would expect that the long term plot would start with full shoe EV at 0 cards pen and EV tend to increase as pen increases. The short term plot should eventually look like the long term plot but since only a relatively small number of shoes are being simulated it will most likely have a relatively large degree of variation. The long term plot could have some variation too but should be far more stable because it is dependent upon computed values so shouldn't require an overwhelming number of simulated shoes in order to see what is happening.
k_c said:
Eric, is it possible for you to organize your data to display 2 plots representing average expected value at each penetration and average actual result of playing each hand with the best decisions? In other words you would be contrasting what has happened short term with what is expected long term.
ericfarmer said:
I suppose I can (I'll take a look tonight)... but I think it would take a lot more than 1000 shoes to get a reasonable comparison. Your 0 pen example illustrates this most clearly; for the expected return it is just a single point, but for the actual return it will be a spread of values. Without having done it yet, I am guessing that with only 1000 samples even the percentile curves will be pretty jumpy.
First sim is 2 decks with cut card placed after 80th card for 10,000 shoes which turned out to be 150,986 rounds.
Simmed EV was ~ +.03% as compared to a full shoe EV ~ -.35%. Simmed difference in EV ~ +.38%
Second sim is 2 decks with cut card placed after 5th card for 100,000 shoes which turned out to be 117,752 rounds.
Simmed EV was ~ -.46% as compared to a full shoe EV ~ -.35%. Simmed difference in EV ~ -.11%
Either one of these simmed EVs may turn out to be more or less for a greater amount of data.
Is there a logical reason why a cut card at position 5 might lose EV while a cut card at position 80 gains EV? The only way 2 rounds can be played with cut card at position 5 is if neither player nor dealer draws even a single card, which means it's likely more high cards than low have been used. This means that whenever a second round is dealt player is forced to play at probably a reduced EV. As more rounds are dealt player has a better opportunity of encountering some +EV rounds. This illustrates that playing blackjack is not quite the same thing as just simply burning a random number of cards in preparation for the next round in which case you might expect more than full shoe EV in the long run at any pen since more info is available.
These sims were done using a program I used to test the .dll version of my CA, which includes a sim function. The test program didn't compute any pre-deal EVs but could have which would slow it up. The test program presently only outputs the results of playing simmed shoes using either best strategy or full shoe basic strategy. I thought that possibly your (Eric's) data might be able to show to at least a beginning extent of how pre-deal EV might vary with pen.
My .dll requires that the user supply shuffled shoes. My test program uses the pseudo random number generator from C++. My theory is that this is good enough for blackjack but in case I am wrong the .dll isn't bound to this. A problem with the prng in C++ is that the distribution of cards can be a little biased because the random number it generates is generally not exactly divisible by a given number of remaining cards when the modulo of remaining cards is used to restrict output to a given range. In order to address this problem I just reject a random number if it is out of range and then recursively generate another number until what is output is not out of range......
unsigned long getRandNum(const unsigned long &max) {
unsigned long maxRand = (unsigned long)(RAND_MAX + 1 - (RAND_MAX + 1) % max);
unsigned long r = (unsigned long)rand();
if (r < maxRand)
return r % max;
else
return getRandNum(max);
}
void shuffle(short specificShoe[], const long &totCards) {
unsigned long i = (unsigned long)totCards;
while (i > 1) {
unsigned long j = getRandNum(i);
short temp = specificShoe[i - 1];
specificShoe[i - 1] = specificShoe[j];
specificShoe[j] = temp;
i--; }
}
Programmatically I wish there was a better way to address this because it is remotely possble that every number may be out of range in which case the program would never finish. Anyway that's how I presently employ the C++ prng and hopefully it gives reasonable results.
Code:
Running simulation
Sim will use the following rules:
bjOdds: 1.5
Dealer stands on soft 17
Double on any 2 cards
Lose only original bet to dealer blackjack (full peek)
No surrender versus up card of ace
No surrender versus up card of ten
No surrender allowed versus up cards 2 through 9
Maximum splits allowed for pairs 2 through 10: 1
Maximum splits allowed for a pair of aces: 1
No doubling after splitting is allowed
Hitting split aces is not allowed
Doubling after splitting aces is not allowed
Press c or C to continue
Press x or X to exit this screen
Continue?
***** pen = 80/104 *****
Setting compute mode (mode setting for sim applies only to that sim)
Press b or B to use basic CD strategy,
any other key for optimal strategy: Optimal strategy
Decks? 2
Number of shoes to sim? 10000
Penetration? 80
Running sim 100.0% complete
Number of decks: 2
Number of rounds: 150986
Number of hands: 154385
Player blackjacks: 7213, expected = 7216.66
Dealer blackjacks: 7320, expected = 7216.66
Total result: 48.5, EV =~ +.032%
Full shoe EV =~ -.35%
Press any key to continue
***** pen = 5/104 *****
Setting compute mode (mode setting for sim applies only to that sim)
Press b or B to use basic CD strategy,
any other key for optimal strategy: Optimal strategy
Decks? 2
Number of shoes to sim? 100000
Penetration? 5
Running sim 100.0% complete
Number of decks: 2
Number of rounds: 117752
Number of hands: 120150
Player blackjacks: 5538, expected = 5628.18
Dealer blackjacks: 5631, expected = 5628.18
Total result: -537.5, EV =~ -.46%
Full shoe EV =~ -.35%
Press any key to continue
k_c said:
First sim is 2 decks with cut card placed after 80th card for 10,000 shoes which turned out to be 150,986 rounds.
Simmed EV was ~ +.03% as compared to a full shoe EV ~ -.35%. Simmed difference in EV ~ +.38%
Second sim is 2 decks with cut card placed after 5th card for 100,000 shoes which turned out to be 117,752 rounds.
Simmed EV was ~ -.46% as compared to a full shoe EV ~ -.35%. Simmed difference in EV ~ -.11%
Either one of these simmed EVs may turn out to be more or less for a greater amount of data.
Simmed EV was ~ +.03% as compared to a full shoe EV ~ -.35%. Simmed difference in EV ~ +.38%
Second sim is 2 decks with cut card placed after 5th card for 100,000 shoes which turned out to be 117,752 rounds.
Simmed EV was ~ -.46% as compared to a full shoe EV ~ -.35%. Simmed difference in EV ~ -.11%
Either one of these simmed EVs may turn out to be more or less for a greater amount of data.
In other words, simply running the same setup again (with a different seed and/or RNG) will likely yield very different results.
Re using std::rand(), I tend not to trust an LCG for statistical stuff. But here also, the most definite way to be sure that your RNG, sample size, etc., is not adversely affecting your results is to simply *run it again* with a different RNG, and verify that your results don't change (to within your desired/quoted accuracy).
I have an easy-to-use Twister implementation (including generating random integers in a specified [0,n) range) that I can pm you if you want.
ericfarmer said:
I think the last statement above is the key. That is, I think 10^5 samples is simply not enough to get a good handle on estimated expected value. If the standard deviation for a round is approximately 1 (and probably higher; WizardOfOdds tells me that it's 1.1418 for a 6-deck round), then even with 150,000 rounds your simmed EV has a sample standard deviation of at least 0.25%.
In other words, simply running the same setup again (with a different seed and/or RNG) will likely yield very different results.
Re using std::rand(), I tend not to trust an LCG for statistical stuff. But here also, the most definite way to be sure that your RNG, sample size, etc., is not adversely affecting your results is to simply *run it again* with a different RNG, and verify that your results don't change (to within your desired/quoted accuracy).
Well, what I was thinking was a graph of computed pre-deal EV versus pen might not require a great deal of data to see a trend. After all we're dealing with computed values and that's as long term as it gets. The only variable is the simmed shoe compositions at he beginning of each round. I think that the starting shoe composition is a pretty powerful force in preventing wild compositions from appearing with a lot of frequency. If that's the case then an overwhelming number of shoes wouldn't seem to be necessary to see the trend.
I agree with you that the validity of results based upon what actually occurs would be questionable without more data. Basically a small amount of this kind of data is showing a shorter term result.
I have an easy-to-use Twister implementation (including generating random integers in a specified [0,n) range) that I can pm you if you want.
In other words, simply running the same setup again (with a different seed and/or RNG) will likely yield very different results.
Re using std::rand(), I tend not to trust an LCG for statistical stuff. But here also, the most definite way to be sure that your RNG, sample size, etc., is not adversely affecting your results is to simply *run it again* with a different RNG, and verify that your results don't change (to within your desired/quoted accuracy).
Well, what I was thinking was a graph of computed pre-deal EV versus pen might not require a great deal of data to see a trend. After all we're dealing with computed values and that's as long term as it gets. The only variable is the simmed shoe compositions at he beginning of each round. I think that the starting shoe composition is a pretty powerful force in preventing wild compositions from appearing with a lot of frequency. If that's the case then an overwhelming number of shoes wouldn't seem to be necessary to see the trend.
I agree with you that the validity of results based upon what actually occurs would be questionable without more data. Basically a small amount of this kind of data is showing a shorter term result.
I have an easy-to-use Twister implementation (including generating random integers in a specified [0,n) range) that I can pm you if you want.
I agree with you that the validity of results based upon what actually occurs would be questionable without more data. Basically a small amount of this kind of data is showing a shorter term result.
ericfarmer said:
I think the last statement above is the key. That is, I think 10^5 samples is simply not enough to get a good handle on estimated expected value. If the standard deviation for a round is approximately 1 (and probably higher; WizardOfOdds tells me that it's 1.1418 for a 6-deck round), then even with 150,000 rounds your simmed EV has a sample standard deviation of at least 0.25%.
In other words, simply running the same setup again (with a different seed and/or RNG) will likely yield very different results.
Re using std::rand(), I tend not to trust an LCG for statistical stuff. But here also, the most definite way to be sure that your RNG, sample size, etc., is not adversely affecting your results is to simply *run it again* with a different RNG, and verify that your results don't change (to within your desired/quoted accuracy).
I have an easy-to-use Twister implementation (including generating random integers in a specified [0,n) range) that I can pm you if you want.
In other words, simply running the same setup again (with a different seed and/or RNG) will likely yield very different results.
Re using std::rand(), I tend not to trust an LCG for statistical stuff. But here also, the most definite way to be sure that your RNG, sample size, etc., is not adversely affecting your results is to simply *run it again* with a different RNG, and verify that your results don't change (to within your desired/quoted accuracy).
I have an easy-to-use Twister implementation (including generating random integers in a specified [0,n) range) that I can pm you if you want.
k_c said:
Well, what I was thinking was a graph of computed pre-deal EV versus pen might not require a great deal of data to see a trend. After all we're dealing with computed values and that's as long term as it gets. The only variable is the simmed shoe compositions at he beginning of each round. I think that the starting shoe composition is a pretty powerful force in preventing wild compositions from appearing with a lot of frequency. If that's the case then an overwhelming number of shoes wouldn't seem to be necessary to see the trend.
I agree with you that the validity of results based upon what actually occurs would be questionable without more data. Basically a small amount of this kind of data is showing a shorter term result.
I agree with you that the validity of results based upon what actually occurs would be questionable without more data. Basically a small amount of this kind of data is showing a shorter term result.
k_c said:
Well, what I was thinking was a graph of computed pre-deal EV versus pen might not require a great deal of data to see a trend. After all we're dealing with computed values and that's as long term as it gets. The only variable is the simmed shoe compositions at he beginning of each round. I think that the starting shoe composition is a pretty powerful force in preventing wild compositions from appearing with a lot of frequency. If that's the case then an overwhelming number of shoes wouldn't seem to be necessary to see the trend.
I agree with you that the validity of results based upon what actually occurs would be questionable without more data. Basically a small amount of this kind of data is showing a shorter term result.
I agree with you that the validity of results based upon what actually occurs would be questionable without more data. Basically a small amount of this kind of data is showing a shorter term result.
Did I miss something?
ericfarmer said:
Hmmm, I may have misunderstood your initial question, then. This sounds like you would like to *sim* a bunch of shoe compositions, but *compute* EV (via CA) for each of those shoes, and look at those trends. If so, then I think we are already on the same page; the blue points in the plot in my initial post were exactly that, computed EVs for corresponding depleted shoes based on simulated heads-up "optimal" play. (Where "optimal" has the usual caveat for splitting; I just used CDZ-.)
Did I miss something?
Did I miss something?

I have played in the past with something similar but for 1deck game where I enumerate all the possible deck compositions at various penetrations. Calculate the probability of each penetration. Calculate the pre-deal EV of each penetration. Group each penetration according based on a running count
The following graphs show the different evs for all the possible compositions at 3 different penetrations for a 1D game (S17) using perfect play composition dependent combinatorial analysis. I however use Running counts instead of True Counts. The graphs on the left hand side show the range of evs for a given RC, while the ones on the right show the sum of weighted EVs (p_i*ev_i).
For the tables:
EN[] give the number of each denomination for composition k
AN[] gives the pre-deal ev, the probability, and the running count of composition k
PenAn[] gives the probability of a running count k, the sum of weighted EVs (p_i*ev_i)
It can be seen clearly that irrespective of the magnitude or sign of the running count, on average we are moving to a positive regime, where at 10 cards remaining in the deck we will be virtually playing with an advantage at all times.



ericfarmer said:
Hmmm, I may have misunderstood your initial question, then. This sounds like you would like to *sim* a bunch of shoe compositions, but *compute* EV (via CA) for each of those shoes, and look at those trends. If so, then I think we are already on the same page; the blue points in the plot in my initial post were exactly that, computed EVs for corresponding depleted shoes based on simulated heads-up "optimal" play. (Where "optimal" has the usual caveat for splitting; I just used CDZ-.)
Did I miss something?
Did I miss something?
Also while you're at it you could plot the corresponding actual results, if they are available, on the same graph which would probably jump all over the place since it is shorter term.
I'm not that good at explaining things but hopefully this is understandable. Basically what I had in mind is just a different way of displaying your data that could maybe display the approximate value of perfect play at each pen level.
P.S.
I don't think the splitting method would make much difference in results.