Standard Deviation

[jaredmt]

how can I figure out my standard deviation based on the counting system I use, what count I play at, and what betting system I use?

is there a formula based on your edge and betting system?

I use wong halves. minimum is $10. @ +2 i bet $20 and add an extra $20 for every true count after that. I truncate the count rather than rounding. Im not entirely sure what my max will be. somewhere between $30 and $100 (probably doesnt help much). I only play when count is at +1 or better. I bet insurance at +3 but i might wait till +3.5 or +4 to lower the SD

all this assuming a regular game where BS player gets .5% disadvantage.

p.s. i did see the SD chart for BS flat betting, but I would think SD is a lot bigger for some one who plays with an advantage and raises bets

 

[FLASH1296]

S.d.

The S.D. for HALVES is listed in Professional Blackjack by Stanford Wong.

Note that it is for the 6 deck S17 game with NDAS so your SD is actually slightly larger, as is your e.v.

As to your assumption re: increased SD due to betting more money, I think that you are correct because the Standard Deviation is the Square of the Varainace.

 

[Sonny]

how can I figure out my standard deviation based on the counting system I use, what count I play at, and what betting system I use?

The most accurate way is with a simulator. Blackjack Attack has an entire chapter filled with results from just about any game you'll find, but it's for HiLo.

-Sonny-

 

[jaredmt]

ok it says win rate is $17 and SD is $426

but benchmark raises bets faster than me. they raise $25 at a time, starting at 0 or +1. i do $20 at a time starting at +2. so I will always have less money on the table until the tc reaches +6, when i hit my max of $100. do you think this will lower the SD a lot? or would it even out to the same since I will probably be playing 8d mostly?

 

[Kasi]

how can I figure out my standard deviation based on the counting system I use, what count I play at, and what betting system I use?

is there a formula based on your edge and betting system?

I don't think edge would matter.

But once you know the frequency the TC's will occur, the advantage associated with each RC and the variance or SD associated with each TC, then yes you can calculate your Stan Dev from that if you want.

And, basically, that's what a sim will do for you and why you need one, like Sonny says, because all those things will change with different games, different pens, different counting systems, use of indexes, etc. There is no formula that will figure freq, adv and sd at each TC. They are what they are once you told the sim everything it needs to know.

But once you have the freq, adv, and sd at each TC, you can pretty much calculate the effect of changing spreads and rolls from there if you want, how SD, risk,N0, and EV etc changes with each different spread without running additional sims for each new spread.

But, really, so what if one can, easy enough to just run another sim if you have one. Plus sims are good at figuring an optimal spread for you giving you the best risk/reward ratio. A good starting point.

But, I sometimes get a little vague on how sims handle multiple hands - covariance issues, wonging out - frequency issues, and maybe even insurance - variance issues lol. Don't worry about it - go with the sim!

 

[Sonny]

so I will always have less money on the table until the tc reaches +6, when i hit my max of $100. do you think this will lower the SD a lot?

It might lower your SD a bit, but it will probably lower your advantage even more. Your short-term swings will be smaller since you're getting less action, but your long-term risk will be greater because your advantage is smaller compared to your variance. That means a higher risk of ruin.

As Kasi said, once you get all the numbers from a sim you can play around with them and see how things change with different bet spreads. This spreadsheet will get you started:

http://www.blackjackinfo.com/bb/showthread.php?p=15578

-Sonny-

 

[jaredmt]

o sweet thanks! i was actually wondering what the frequencies of each TC were too. and I think with this info, I can attempt to write my own program for my own spread, br, and unit size when/if I have the time or the patience lol.

i guess with the 1.33 variance, that means on average you win/lose 1 unit 2/3 of the time and win/lose 2 units 1/3 of the time right? I have basic programming skills so it would be easier for me to calculate everything with %s rather than running through each card and each play.

 

[callipygian]

I don't think edge would matter.

EV does matter because SD uses (actual-expected) as a term in its calculation. For any system, you need to calculate the EV first before you can calculate SD.

But once you know the frequency the TC's will occur, the advantage associated with each RC and the variance or SD associated with each TC, then yes you can calculate your Stan Dev from that if you want ... I sometimes get a little vague on how sims handle multiple hands - covariance issues, wonging out - frequency issues, and maybe even insurance - variance issues lol. Don't worry about it - go with the sim!

SD's can be calculated from the win-loss percentages for every combination of player cards vs. dealer cards. It's just sqrt[ Sum {P(i,j)*((%win(i,j)*Bet(i,j) - EV(i,j))^2-(%lose(i,j)*Bet(i,j)-EV(i,j)))}].

 

[callipygian]

i was actually wondering what the frequencies of each TC were too.

That depends on the number of decks and the penetration.

i guess with the 1.33 variance, that means on average you win/lose 1 unit 2/3 of the time and win/lose 2 units 1/3 of the time right?

No, it would mean that 68% of the time, your actual result will fall within sqrt(1.33) units of your expected result, and 95% of the time, your actual result will fall within 2*sqrt(1.33) of your expected result. SD = sqrt(variance).

Note that a 1.33 variance is pretty low. Sonny gave me a ballpark figure of SD = 2.5 to 3 for most counters; I've found through my own calculations that SD's can go as low as 2 under some Wonging conditions. These would correspond with variances of 4 to 9 ... a variance of 1.33 corresponds to a SD of 1.15, which is flat betting.

 

[Sonny]

EDIT: See calliphygian's corrections to this post below

For any system, you need to calculate the EV first before you can calculate SD.

If you’re calculating the variance through simulation (instead of a population of known data points) you don’t necessarily need to calculate the mean (EV) first. In the case of most gambling games you can just take the average squared result. For example, the pseudo-code for calculating the variance of a coin toss might look something like this:

for (rounds = 0; rounds < N; rounds ++)
{
   Result = Random Number (0|1);
   If (Result == 0){
      Win = WinPayout;
}
   else {
      Win = LossPayout;
}
   Bankroll += Win
   Variance += Win^2;
}

VariancePerHand = Variance/N;
SDPerHand = Sqrt(VariancePerHand);

-Sonny-

 

[callipygian]

In the case of most gambling games you can just take the average squared result.

You're basically assuming that EV = 0 in this case (the formula for variance is technically (Win-EV)^2); it works when EV's actually are pretty close to 0 and no decisions need to be made (e.g. craps), but in blackjack, that's not always the case, because EV's for individual hands range from -0.5 (surrender) to +0.79 (hard 20 vs. dealer 8) and decisions need to be recalculated for each hand.

For a lot of hands, this assumption will hold - for instance, hard 17 vs. 6 the variance will be exactly the same either way because EV = 0, but for others, hard 16 vs. 10 the variance will differ greatly (using your pseudocode, surrendering hard 16 vs. 10 carries a non-zero variance when it should be zero).

 

[Sonny]

You're basically assuming that EV = 0 in this case (the formula for variance is technically (Win-EV)^2);

Yeah, I realized that as soon as I posted (then deleted the post hoping nobody read it). I copied that code from one of my programs, then noticed that farther down in the program was the line: Variance -= EV^2. I simplified it by removing the overall EV at the very end of the program instead of individual EVs after each hand. I suppose the overall difference would be indetectable in cases where the player's EV is small (like card counting), but to be completely accurate you need to adjust for the EV.

I guess I'll un-delete my previous post since you caught my mistake before I did (again).

-Sonny-

 

[callipygian]

Yeah, I realized that as soon as I posted (then deleted the post hoping nobody read it).

If you hadn't put in the edit tags, I wouldn't have known anything changed.

 

[Kasi]

EV does matter because SD uses (actual-expected) as a term in its calculation. For any system, you need to calculate the EV first before you can calculate SD.
SD's can be calculated from the win-loss percentages for every combination of player cards vs. dealer cards. It's just sqrt[ Sum {P(i,j)*((%win(i,j)*Bet(i,j) - EV(i,j))^2-(%lose(i,j)*Bet(i,j)-EV(i,j)))}].

Well, just as a follow-up, maybe I'm just used to sim results, mayb elike Sonny was saying, or even something as you suggest every possible combination of cards would be the ultimate lol.

I'm just trying to say the HA will fall-out from the freq of net wins and losses of various amounts. Like in the Wiz's Appendix 4. All you need are the first 2 columns to figure out a SD of (at least I get) 1.14180297008499 and the house edge for that defined game.

It just seems the frequency of a net win or loss of various amounts, given rules of a game, maybe comes first, that that is all one needs?

Like the only way to know what a rule may cost, and also what the SD is for that game, is to know how often a net win of whatever will occur?

Maybe we're probably saying the same in different ways lol since maybe the way the Wiz produced his table was to do exactly what you were suggesting and summarizing it? But even at the micro-level of a specific hand, you don't know what the right play is, hit or stand, until you know how often it occurs vs a dealer card, etc?

 

[callipygian]

I'm just trying to say the HA will fall-out from the freq of net wins and losses of various amounts. Like in the Wiz's Appendix 4. All you need are the first 2 columns to figure out a SD of (at least I get) 1.14180297008499 and the house edge for that defined game.

Yes, this is true. However, when you change the game (say, by doubling your bet at counts of +1 or more) then what happens is that the percentage wins FOR EACH HAND change. As a result, you need to recalculate Appendix 4 for every true count; then, you have to multiply each of the variances by the amount you bet at that count; then, you have to normalize the set of variances by the percentage of time that you are playing at that count. When you add them all up, you get your total variance, and then take the square root of that for your total SD.

 

[sagefr0g]

It might lower your SD a bit, but it will probably lower your advantage even more. Your short-term swings will be smaller since you're getting less action, but your long-term risk will be greater because your advantage is smaller compared to your variance. That means a higher risk of ruin.

As Kasi said, once you get all the numbers from a sim you can play around with them and see how things change with different bet spreads. This spreadsheet will get you started:

http://www.blackjackinfo.com/bb/showthread.php?p=15578

-Sonny-

Sonny on your spread sheet a couple of questions.

you use variance in your spread sheets column D . would it make sense if you had a simulation that gives the standard deviations at those corresponding true counts to figue the variance from those standard deviations and then plug those variance numbers into your spread sheet instead of the number you use. also was wondering why you use a variance = 1 for the negative tc's.

also what is this variance in column D anyway.
is it variance of the TC or variance of the frequency of the TC or is it variance of EV at a TC ?

 

[Kasi]

Yes, this is true. However, when you change the game (say, by doubling your bet at counts of +1 or more) then what happens is that the percentage wins FOR EACH HAND change. As a result, you need to recalculate Appendix 4 for every true count; then, you have to multiply each of the variances by the amount you bet at that count; then, you have to normalize the set of variances by the percentage of time that you are playing at that count. When you add them all up, you get your total variance, and then take the square root of that for your total SD.

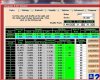
Well OK. It still just sounds like if the Wiz table had all the net wins of -8 to 8 for that game by each TC and their frequencies as you suggest, the advantage and variance at each TC would fall out in the same way it did in the Wiz table.

So, to get back to my original point, I can see edge enters into the calc eventually maybe but I don't see why needing to know it in advance is some kind of pre-requisite. I don't even see how you could even know the edge in advance.

Is there anything in what you suggest above that requires you to know the edge initially? Need you not know anything more than freq of net wins and their pay-offs at each TC?

I only included all those decimals above so, if I did it right, the way I think you are suggesting, you can see I did use the edge in the calculation and it was hard to tell from the Wiz result exactly what he did since the edge makes so little difference in this case. Is that what you would get? I always feel better if someone can confirm anything I do lol.

I guess I always assumed when a sim gives me the variance and adv at each TC that in effect it already worked out a series of "Wiz tables" like above except for each TC. And, when combined, basically would end up with a summary Wiz table like in his appendix? All always assuming a 1 unit initial bet per round.

What do sims do - do they subtract out the EV^2 of that particular TC when they give you variance or SD at a TC like, say, in CH10? Did they need to know the edge in the first place?

After that, if you want to bet 10 units at +10 or -10, your avg initial bet unit will obviously have changed. So also will have your avg overall EV.

But, am I wrong? - I'm just asking and it sure wouldn't be the first time, that's for darn sure - in thinking even God couldn't change the freq and net unit wins at each TC individually, given the usual stuff of count system, etc and also overall?

Assume what you want but the game itself can't change - you'll always have a net win of so many units so often from a 1 unit initial bet.

Do I need to know anything more to calc variance, say in roulette, than 20/38of the time I'll lose 1 unit on red and 18/38 of the time I won't with a 1-1 pay off to know that my variance is 0.99723 per spin? If I know those frequencies and net wins, I'll know the edge too in the process won't I? If the rules of the game allowed red to be paid at 2-1, all I still need to know to calc variance is how often a winning bet will occur compared to a losing bet?

Anyway, broadly speaking, that's why I think, mistakenly or not, to paraphrase Tina, "what's edge got to do with it?"

 

[Kasi]

Sonny on your spread sheet a couple of questions...QUOTE]

I'm not saying anything about his sheet, not even sure what you're asking lol, but, if I remember right, he's just assuming an avg variance for an avg BJ game. Why, if so, just 1 at <0, I have no idea. Makes no sense to me. Maybe it doesn't matter anyway if it's for some back-counting scenario and he'd never play a -TC hand anyway?

Of course it's better to run a sim, it's more accurate. But, no doubt, Sonny's methodology would still apply. I'll take his methodology over mine any day lol.

I think, not sure, generally, + counts will have less variance for each +TC compared to neutral and more variance at each -TC compared to neutral.

Obviously the variance in real life would never actually be a constant at every +TC. Can't happen. Likewise it never would get as low as 1 in - counts. I think it's intended more for methodology than "accuracy" per se.

I looked at his sheet once a long time ago and he answered a few questions I asked, since, like you maybe, I did have some q's lol. Can't find the thread though lol.

 

[sagefr0g]

Sonny on your spread sheet a couple of questions...QUOTE]

I'm not saying anything about his sheet, not even sure what you're asking lol, but, if I remember right, he's just assuming an avg variance for an avg BJ game. Why, if so, just 1 at <0, I have no idea. Makes no sense to me. Maybe it doesn't matter anyway if it's for some back-counting scenario and he'd never play a -TC hand anyway?

Of course it's better to run a sim, it's more accurate. But, no doubt, Sonny's methodology would still apply. I'll take his methodology over mine any day lol.

I think, not sure, generally, + counts will have less variance for each +TC compared to neutral and more variance at each -TC compared to neutral.

Obviously the variance in real life would never actually be a constant at every +TC. Can't happen. Likewise it never would get as low as 1 in - counts. I think it's intended more for methodology than "accuracy" per se.

I looked at his sheet once a long time ago and he answered a few questions I asked, since, like you maybe, I did have some q's lol. Can't find the thread though lol.

yeah so i guess the variance or standard deviation a sim gives us is an average, i'm just still wondering just what the standard deviation refers to or like in Sonny's spreadsheet what the variance refers to.
ie. standard deviation of what or variance of what?
like in the sim image below, i think standard deviation in the upper field refers to standard deviation of the winrate per hand and winrate per hour.
but i'm lost on what the standard deviation refers to in the column where there is a standard deviation associated with each TC.
i'm guessing it must be for either TC frequency or EV, or maybe both?

edit: ===>>> oh ok i think this post shows what the variance refers to. EV i believe from the sound of it:
http://www.blackjackinfo.com/bb/showpost.php?p=102358&postcount=12

 

[Kasi]

yeah so i guess the variance or standard deviation a sim gives us is an average, i'm just still wondering just what the standard deviation refers to or like in Sonny's spreadsheet what the variance refers to.
ie. standard deviation of what or variance of what?
like in the sim image below, i think standard deviation in the upper field refers to standard deviation of the winrate per hand and winrate per hour.
but i'm lost on what the standard deviation refers to in the column where there is a standard deviation associated with each TC.
i'm guessing it must be for either TC frequency or EV, or maybe both?

edit: ===>>> oh ok i think this post shows what the variance refers to. EV i believe from the sound of it:
http://www.blackjackinfo.com/bb/showpost.php?p=102358&postcount=12

Well, what I think, which may not be right lol, is that the SD's in col 3, anything close to 1.15 whatever column it's in, is the SD that occurs assuming a flat bet at that TC (given counting sys, pen, how TC calced, use of indexes, etc).

The SD given in a sim, after one specifies how much to bet at what count, just falls out from the former. If you change your spread, the SD in that upper level will change too. So will the EV%.

The SD's and EV% in those upper levels are just averages per round to make life easier so all you need to know to know your EV and SD is how many rounds you have played. You don't need to know how many rounds you've played at each TC on the assumption it will all avg out in the end.

Basically it's why, if backcounting, there's really not much point in spreading 1-20 compared to 1-4 with same roll. At 1-20 you have a lower min unit compared to 1-4. At 1-20 your max $ bet is lower (I think?) compared to 1-4. Your win rate though is essentially uneffected with same risk to roll. So why bother with 1-20, it gains you, basically, nothing.

SD per round has nothing to do with win rate per round per se. If you change how many units you bet at each count, both will change.

I don't know - just free-forming it late at night lol.