ericfarmer said:
I suppose I can (I'll take a look tonight)... but I think it would take a lot more than 1000 shoes to get a reasonable comparison. Your 0 pen example illustrates this most clearly; for the expected return it is just a single point, but for the actual return it will be a spread of values. Without having done it yet, I am guessing that with only 1000 samples even the percentile curves will be pretty jumpy.
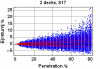
I ran 2 sims in which player uses optimal strategy for the current composition. The only decision that is possibly not optimal is the decision of splitting but in the great majority of cases, if not all cases, the best decision will have been made. (Split EV is figured as playing the first split hand optimally and applying the same strategy to the second hand. The second hand in the sim will actually be played with knowledge of what was drawn on the first hand so actual split EV should be marginally greater than computed EV in the long run. Rules in sim allow for only 1 split)
First sim is 2 decks with cut card placed after 80th card for 10,000 shoes which turned out to be 150,986 rounds.
Simmed EV was ~ +.03% as compared to a full shoe EV ~ -.35%. Simmed difference in EV ~ +.38%
Second sim is 2 decks with cut card placed after 5th card for 100,000 shoes which turned out to be 117,752 rounds.
Simmed EV was ~ -.46% as compared to a full shoe EV ~ -.35%. Simmed difference in EV ~ -.11%
Either one of these simmed EVs may turn out to be more or less for a greater amount of data.
Is there a logical reason why a cut card at position 5 might lose EV while a cut card at position 80 gains EV? The only way 2 rounds can be played with cut card at position 5 is if neither player nor dealer draws even a single card, which means it's likely more high cards than low have been used. This means that whenever a second round is dealt player is forced to play at probably a reduced EV. As more rounds are dealt player has a better opportunity of encountering some +EV rounds. This illustrates that playing blackjack is not quite the same thing as just simply burning a random number of cards in preparation for the next round in which case you might expect more than full shoe EV in the long run at any pen since more info is available.
These sims were done using a program I used to test the .dll version of my CA, which includes a sim function. The test program didn't compute any pre-deal EVs but could have which would slow it up. The test program presently only outputs the results of playing simmed shoes using either best strategy or full shoe basic strategy. I thought that possibly your (Eric's) data might be able to show to at least a beginning extent of how pre-deal EV might vary with pen.
My .dll requires that the user supply shuffled shoes. My test program uses the pseudo random number generator from C++. My theory is that this is good enough for blackjack but in case I am wrong the .dll isn't bound to this. A problem with the prng in C++ is that the distribution of cards can be a little biased because the random number it generates is generally not exactly divisible by a given number of remaining cards when the modulo of remaining cards is used to restrict output to a given range. In order to address this problem I just reject a random number if it is out of range and then recursively generate another number until what is output is not out of range......
unsigned long getRandNum(const unsigned long &max) {
unsigned long maxRand = (unsigned long)(RAND_MAX + 1 - (RAND_MAX + 1) % max);
unsigned long r = (unsigned long)rand();
if (r < maxRand)
return r % max;
else
return getRandNum(max);
}
void shuffle(short specificShoe[], const long &totCards) {
unsigned long i = (unsigned long)totCards;
while (i > 1) {
unsigned long j = getRandNum(i);
short temp = specificShoe[i - 1];
specificShoe[i - 1] = specificShoe[j];
specificShoe[j] = temp;
i--; }
}
Programmatically I wish there was a better way to address this because it is remotely possble that every number may be out of range in which case the program would never finish. Anyway that's how I presently employ the C++ prng and hopefully it gives reasonable results.
Code:
Running simulation
Sim will use the following rules:
bjOdds: 1.5
Dealer stands on soft 17
Double on any 2 cards
Lose only original bet to dealer blackjack (full peek)
No surrender versus up card of ace
No surrender versus up card of ten
No surrender allowed versus up cards 2 through 9
Maximum splits allowed for pairs 2 through 10: 1
Maximum splits allowed for a pair of aces: 1
No doubling after splitting is allowed
Hitting split aces is not allowed
Doubling after splitting aces is not allowed
Press c or C to continue
Press x or X to exit this screen
Continue?
***** pen = 80/104 *****
Setting compute mode (mode setting for sim applies only to that sim)
Press b or B to use basic CD strategy,
any other key for optimal strategy: Optimal strategy
Decks? 2
Number of shoes to sim? 10000
Penetration? 80
Running sim 100.0% complete
Number of decks: 2
Number of rounds: 150986
Number of hands: 154385
Player blackjacks: 7213, expected = 7216.66
Dealer blackjacks: 7320, expected = 7216.66
Total result: 48.5, EV =~ +.032%
Full shoe EV =~ -.35%
Press any key to continue
***** pen = 5/104 *****
Setting compute mode (mode setting for sim applies only to that sim)
Press b or B to use basic CD strategy,
any other key for optimal strategy: Optimal strategy
Decks? 2
Number of shoes to sim? 100000
Penetration? 5
Running sim 100.0% complete
Number of decks: 2
Number of rounds: 117752
Number of hands: 120150
Player blackjacks: 5538, expected = 5628.18
Dealer blackjacks: 5631, expected = 5628.18
Total result: -537.5, EV =~ -.46%
Full shoe EV =~ -.35%
Press any key to continue