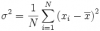Variance is actually a fairly simple concept. The statisticians just make it sound hard!

For any group of numbers there is a mean (often called the average). For example:
2,4,7,9,5,1,5,7
The average of the above numbers is 5, but most of the numbers are either higher or lower than 5. Knowing the average really doesn’t tell us much about this group. We also want to know how far away the numbers are from the mean. That is where variance helps us.
To calculate the variance of a group, just subtract the mean from the number and square the value. This will give you the variance for each individual entry. Then add up all of the individual variances and divide by the total number of entries. Essentially, you are calculating the “average squared difference” of the numbers from the mean. Here’s how it works for the example above:
(Number – Mean)^2 = var
2-5=-3^2=9
4-5=-1^2=1
7-5=2^2=4
9-5=4^2=16
5-5=0^2=0
1-5=-4^2=16
5-5=0^2=0
7-5=2^2=4
TOTAL = 50
AVERGAGE = 50 / 8 = 6.25
Var = 6.25
SD = 2.5
The variance doesn’t really help us much so we convert it to standard deviations by taking the square root: 2.5. This gives us a general idea of how far the results were from the mean. In this case they were all pretty close so the variance is low, but let’s take another example:
3,78,32,89,2,56,79,5
The mean is now 344 / 8 = 43. The variance is:
3-43=-40^2=1600
78-43=35^2=1225
32-43=-11^2=121
89-43=46^2=2116
2-43=-41^2=1681
56-43=13^2=169
79-43=36^2=1296
5-43=-38^2=1444
TOTAL = 9652
AVERGAGE = 9652 / 8 = 1206.5
Var = 1206.5
SD = 34.73
The variance is much higher because many of the entries were far from the mean. Knowing the variance showed us that there were large fluctuations in this group and that the mean was somewhat misleading. Instead of always expecting a result of 43 every time, we know that our actual results will vary greatly.
There are many different formulas for variance that are used for different types of data. The one above is the simplest and most intuitive. Hopefully it will help you to understand the concept of variance and SD.
-Sonny-
P.S. - Now wasn't that much easier than this: