Rc 2 tc
- Thread starter aneuzil21
- Start date
ccibball50
Well-Known Member
a
I do it just before I act if I have cards that could be affeted by the count, and at the end of each round so I will know how much to bet. I calculate by using half decks for 6 deck, and quarter deck for SD and DD. I remember stuff wierd, so I have wierd ratios that I use which makes it easier for me.
I do it just before I act if I have cards that could be affeted by the count, and at the end of each round so I will know how much to bet. I calculate by using half decks for 6 deck, and quarter deck for SD and DD. I remember stuff wierd, so I have wierd ratios that I use which makes it easier for me.
jack.jackson
Well-Known Member
Believe it or not, this is actually how I calculate my TC for MD. Furthermore, I dont miss a beat. This differs drastically from the method I use for DD and Single deck!aneuzil21 said:With HILO 6-Deck shoe, how often do you calculate the TC? After each deck? Do you use fractions or round to a conservative figure?
The reason I do it this way, is because I hate trying to divide, "let's say" +15 by 2.5 decks, which is a +6, correct. I use a level2.
Instead of dividing by 2.5, I like to divide by 5, then multiplyx2
5/15=+3x2=+6
Note however an alternative would be just to reduce my indices to half their value, and drop the x2 step. The reason I dont do this, is because 1) I would've had to relearn all my indices(however simple) and 2)I dont like, 1/2 indices(2.5,5.5,etc).
Anyway I turn the 6decks, into twelve 1/2 decks. So if my RC, is between -5 and -9 with 1 deck in the discard tray my TC is -1
If my my RC was -10, my TC would now be -2. -10/10=-1x2=-2
(I think this is truncating)
Moving on:
Now everybody calculates their TC at the same time for betting, but I think this differs for some counters, when it comes to playing their hand. For example, "I think" some beginners use the same TC for playing their hand as they did for betting their hand. I guess this would depend if the game was face up or not, and the actual method being used, and/or seat location.
Last edited:
Sonny
Well-Known Member
That's a good trick. I usually just multiply by 0.4 (multiply by 4 and move the decimal place).jack said:Instead of dividing by 2.5, I like to divide by 5, then multiplyx2
5/15=+3x2=+6
15*4 = 60 (slide decimal place over 1 spot) = 6.0
-Sonny-
FLASH1296
Well-Known Member
You constantly re-calculate.
Do not "round" your True Count.
The immortal Peter Griffin stated that If one plays their +3 Basic Strategy Variations at +2,
they will do WORSE than someone not using any indices at all. See Theory of Blackjack.
You should "FLOOR" your True Count computations, as do nearly all published experts.
POSITIVE True Counts get cut off at the first digit, so +2.1 to + 2.9 are all T.C. +2
NEGATIVE True Counts get dropped to the next lower digit, so -2.1 to - 2.9 are all T.C. -3
Do not "round" your True Count.
The immortal Peter Griffin stated that If one plays their +3 Basic Strategy Variations at +2,
they will do WORSE than someone not using any indices at all. See Theory of Blackjack.
You should "FLOOR" your True Count computations, as do nearly all published experts.
POSITIVE True Counts get cut off at the first digit, so +2.1 to + 2.9 are all T.C. +2
NEGATIVE True Counts get dropped to the next lower digit, so -2.1 to - 2.9 are all T.C. -3
QFIT
Well-Known Member
Some additional minutia: http://www.qfit.com/CalculatingTrueCounts.htm
SleightOfHand
Well-Known Member
Woah, really? Just using common sense, it seems that using slightly incorrect indeces, while damaging to your win rate, would still be greater than no indeces at all.FLASH1296 said:The immortal Peter Griffin stated that If one plays their +3 Basic Strategy Variations at +2,
they will do WORSE than someone not using any indices at all. See Theory of Blackjack.
Logic (or not): Incorrect deviations are only incorrect at the area in between the correct and incorrect index (making the wrong play between +2 and +3 in your case). The loss in advantage in this area is less than the gain in advantage from +3 and upwards. So the total change in advantage is still positive. Therefore, while it hurts you to deviate incorrectly, as long as it isn't significant, "incorrect" deviations are still +EV. I put incorrect in quotes because it makes me think about RA indexes that are "incorrect". Looking at a page of QFITs website shows that the advantage vs TC graphs for a few situations, while not linear, are at least close enough for my "logic" to be acceptable. Of course, if other situations are not like this, you can just scrap my post.
PS: I just realized that perhaps the percentage of the time that we are between +2 and +3 rather than >+3 may be the major fault in my logic. Using the canned sim for HiLo S16F4 shows we are between +2 and +3 about 7.4% of the time and higher about 8% of the time (play all). I suppose that by multiplying the individual frequencies by the TC in QFITs graphs would give a much more hyperbolic (actually its something i dont know what to call(normal curve * linear)) graph which is most likely to be the reason why Flash's statement is true (if such is the case). So yea, I guess I was wrong lol. Answered myself! Weeeee!
Last edited:
callipygian
Well-Known Member
There's an even easier trick - learn multiplication tables for non-integers.Sonny said:That's a good trick.
Let's say you have an RC of +23 and 4.5 decks remaining. If you have 4.5 x 5 = 22.5 memorized, it's not a huge trick to estimate the TC at 5, especially if you floor the TC (as you should).
You don't need to memorize that many ... 1.5 x 2 through 4.5 x 5 (16 entries) for shoe games. On an 8-deck shoe, 5.5 tables might come in handy too, but the chances you're going to use them are pretty rare.
And honestly, the chances that you'll need this in places other than the casino is pretty high ... if Ho-Hos are $5 for 2 boxes, how many boxes can you buy with $12? It's the same calculation.
SleightOfHand
Well-Known Member
I may be weird, but I...
Ex: My index for 9v2 is +2. If the RC is +10, then 10/2=5. I then look at the discard tray and if there are 5 or fewer decks remaining (1 or more decks dealt), then I double. Im not sure if this is a popular method, I heard this was in BBiBJ, although I don't recall it. I like it because I dont have to deal with dividing fractions. The drawback is that you have to do an additional computation (Total decks-decks remaining), although I dont find it problematic.
take the RC and divide it by the index to see the required remaining decks to make the deviation.callipygian said:There's an even easier trick - learn multiplication tables for non-integers.
Let's say you have an RC of +23 and 4.5 decks remaining. If you have 4.5 x 5 = 22.5 memorized, it's not a huge trick to estimate the TC at 5, especially if you floor the TC (as you should).
You don't need to memorize that many ... 1.5 x 2 through 4.5 x 5 (16 entries) for shoe games. On an 8-deck shoe, 5.5 tables might come in handy too, but the chances you're going to use them are pretty rare.
And honestly, the chances that you'll need this in places other than the casino is pretty high ... if Ho-Hos are $5 for 2 boxes, how many boxes can you buy with $12? It's the same calculation.
Ex: My index for 9v2 is +2. If the RC is +10, then 10/2=5. I then look at the discard tray and if there are 5 or fewer decks remaining (1 or more decks dealt), then I double. Im not sure if this is a popular method, I heard this was in BBiBJ, although I don't recall it. I like it because I dont have to deal with dividing fractions. The drawback is that you have to do an additional computation (Total decks-decks remaining), although I dont find it problematic.
jack.jackson
Well-Known Member
About a 1 year ago, Bojack suggested that I try it this way. A couple reasons why I didnt try it this way is 1) i was used do doing it my way, and 2) lets say your RC was +18 with 2 1/2 decks left.Sonny said:That's a good trick. I usually just multiply by 0.4 (multiply by 4 and move the decimal place).
15*4 = 60 (slide decimal place over 1 spot) = 6.0
-Sonny-
Multiplying 18x4, and taking 1/10 that, would be tougher for me, than taking dividing 5/18,= 33/5x2
(note that as long as my numerator is more than 1/2 my denominator it will =+7)when a RC of +17(3 2/5) would still be considered +6.
This way may seem a little tougher to you, but its really not that bad. Now wheres those Ho,Ho's.
sagefr0g
Well-Known Member
that's a pretty cool trick.SleightOfHand said:take the RC and divide it by the index to see the required remaining decks to make the deviation.
Ex: My index for 9v2 is +2. If the RC is +10, then 10/2=5. I then look at the discard tray and if there are 5 or fewer decks remaining (1 or more decks dealt), then I double. Im not sure if this is a popular method, I heard this was in BBiBJ, although I don't recall it. I like it because I dont have to deal with dividing fractions. The drawback is that you have to do an additional computation (Total decks-decks remaining), although I dont find it problematic.
one thing, is the index for 9v2 +1?
Pelerus
Well-Known Member
In shoe games (which is what I have played so far), I estimate to the nearest deck rather than half or quarter deck - so I never have to divide by a non-integer.
In fact, when calculating the TC, I do not actually divide at all, per se: rather, I reason that if 4 decks remain, I need a RC of +4 to make a TC of +1, +8 to make +2, etc. So if my RC is +6, I have a TC of +1 (for betting and playing purposes), because I have not yet reached +8 RC.
This gives equivalent results to flooring (for positive counts), but I find the mental process easier than thinking, in the same example above: "+6 divided by 4 equals 1.5, rounded down is 1."
But because flooring requires rounding up (by absolute value) in negative decks, I simply alter the process somewhat: if 4 decks remain, I only need a RC of -5 to make a TC of -2, a RC of -9 to make -3, etc. So if my RC is -6, I have a practical TC of -2.
In fact, when calculating the TC, I do not actually divide at all, per se: rather, I reason that if 4 decks remain, I need a RC of +4 to make a TC of +1, +8 to make +2, etc. So if my RC is +6, I have a TC of +1 (for betting and playing purposes), because I have not yet reached +8 RC.
This gives equivalent results to flooring (for positive counts), but I find the mental process easier than thinking, in the same example above: "+6 divided by 4 equals 1.5, rounded down is 1."
But because flooring requires rounding up (by absolute value) in negative decks, I simply alter the process somewhat: if 4 decks remain, I only need a RC of -5 to make a TC of -2, a RC of -9 to make -3, etc. So if my RC is -6, I have a practical TC of -2.
Pelerus
Well-Known Member
He may be using Zen indices (which is what I am now using), in which case 9v2 is doubled at +2 as he said.sagefr0g said:that's a pretty cool trick.
one thing, is the index for 9v2 +1?
zengrifter
Banned
Can we get independent confirmation on this? I don't have the book handy. zgFLASH1296 said:Do not "round" your True Count.
The immortal Peter Griffin stated that If one plays their +3 Basic Strategy Variations at +2,
they will do WORSE than someone not using any indices at all. See Theory of Blackjack.
sagefr0g
Well-Known Member
better late than early
at least that's my take on what he's explaining.
for example he's saying:
"... that if the critical threshold value is +3, the player who changes strategy for +2 or above will lose more than the basic strategist ( who never changes), and will lose more than the perfect employer of the system can gain...."
explaining this Griffin is pointing out the non-linearity nature of the advantage of changing plays, at least thats the drift, i'm gettin, but i didn't read the whole chapter.
Quote:
Originally Posted by FLASH1296
Do not "round" your True Count.
The immortal Peter Griffin stated that If one plays their +3 Basic Strategy Variations at +2,
they will do WORSE than someone not using any indices at all. See Theory of Blackjack
page 107 has some referance to the problem of making matrice plays to early, where Griffin points out it's worse than never taking them.zengrifter said:Can we get independent confirmation on this? I don't have the book handy. zg
at least that's my take on what he's explaining.
for example he's saying:
"... that if the critical threshold value is +3, the player who changes strategy for +2 or above will lose more than the basic strategist ( who never changes), and will lose more than the perfect employer of the system can gain...."
explaining this Griffin is pointing out the non-linearity nature of the advantage of changing plays, at least thats the drift, i'm gettin, but i didn't read the whole chapter.
QFIT
Well-Known Member
Between rounding, truncation and flooring, generally you want to do what the author did when he generated the indexes. Unfortunately, authors don't tell you this. They also don't tell you the remaining decks accuracy that was used during generation. I once looked through all the books trying to figure out what they did, and although it isn't clear, they have used various methods.
The chart below uses the full indexes in the back of Wong's 1994 edition of PBJ. Wong truncated when he created these. I ran it with truncation, flooring and rounding and also no indexes.
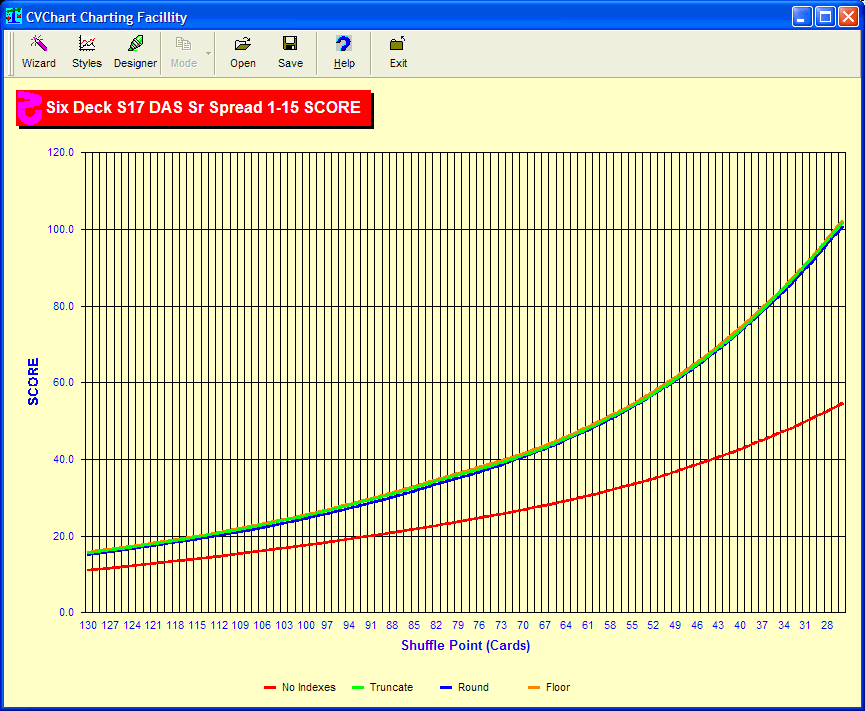
The differences are quite small with flooring coming out on top. This is with about 140 indexes. With the Illustrious 18, the differences would be less. It should also be noted that there are errors in the PBJ indexes.
For a chart on how often you should recalculate True Counts, see http://www.blackjackincolor.com/penetration9.htm
The chart below uses the full indexes in the back of Wong's 1994 edition of PBJ. Wong truncated when he created these. I ran it with truncation, flooring and rounding and also no indexes.

The differences are quite small with flooring coming out on top. This is with about 140 indexes. With the Illustrious 18, the differences would be less. It should also be noted that there are errors in the PBJ indexes.
For a chart on how often you should recalculate True Counts, see http://www.blackjackincolor.com/penetration9.htm
Interesting
Apparantly, I've been "flooring," but wasn't up on the lingo yet. It just seems that people make it more difficult than necessary. I.E. If we have a a RC of + 18 with 2.5 decks remaining, I would go with +6 to be conservative. 18/3 = 6 or 18/2 = 9. If you weren't playing with any indeces at all, you would still bet according to a +6 count. In other words, no hit on 16, 15, etc.
Maybe I'm missing something.
Apparantly, I've been "flooring," but wasn't up on the lingo yet. It just seems that people make it more difficult than necessary. I.E. If we have a a RC of + 18 with 2.5 decks remaining, I would go with +6 to be conservative. 18/3 = 6 or 18/2 = 9. If you weren't playing with any indeces at all, you would still bet according to a +6 count. In other words, no hit on 16, 15, etc.
Maybe I'm missing something.
Priorities
Staying under the radar seems to be more challenging by the day. For that reason, I devote more "brain power" to that and try to keep other things such as this as simple as possible while still effective.
This subject is important but if I can't play it doesn't matter how masterfully I can do these things.
Billy C1
Staying under the radar seems to be more challenging by the day. For that reason, I devote more "brain power" to that and try to keep other things such as this as simple as possible while still effective.
This subject is important but if I can't play it doesn't matter how masterfully I can do these things.
Billy C1
jack.jackson
Well-Known Member
Youre right on
Sorry if I got a little carried away in my explanation. I have a bad habit of doing that sometimes. It's one of the reason's, I havent brought it up, in the two years as a member here. It was more for show, than anything else :smile: . And yes, you're right! simple is the best policy. Another simple approach, is to just take a fraction of the RC, depending on how deep in the deck you are.
Good Luck!
aneuzil21 said:Apparantly, I've been "flooring," but wasn't up on the lingo yet. It just seems that people make it more difficult than necessary. I.E. If we have a a RC of + 18 with 2.5 decks remaining, I would go with +6 to be conservative. 18/3 = 6 or 18/2 = 9. If you weren't playing with any indeces at all, you would still bet according to a +6 count. In other words, no hit on 16, 15, etc.
Maybe I'm missing something.
Sorry if I got a little carried away in my explanation. I have a bad habit of doing that sometimes. It's one of the reason's, I havent brought it up, in the two years as a member here. It was more for show, than anything else :smile: . And yes, you're right! simple is the best policy. Another simple approach, is to just take a fraction of the RC, depending on how deep in the deck you are.
Good Luck!
jack.jackson
Well-Known Member
I can honestly tell you first hand, I can personally attest to this. Take Bryce Carlson, in BJFB for example, with his 11vX index, which is -6. I guarantee you that if you hit this @-7 with 2D or less(especially 1D or less)remaining you're losing money. If you're fortunate enough to get down to 1/2 deck to go, you can double this play ALL-DAY long @ RC-6(TC-12) and still nail those tens. Its also one of the reasons, I find myself being extremely conservartive with the Ao2s negative indices, deep in the deck. If you try and hit 13v3(-4) @ -5 w/1D remaining your gonna pay for it! But yet, this index seems to work perfectly with 4D remaining. I really wish I knew, how many decks Carlson used to generate his indices, because I can assure you their far from perfect! Unsure if its the floating advantage causing these inaccuricies, or if its, that they, were created with a compromise for any number decks in mind. Its one of the reasons, I dropped a 160$ bucks on CVData.qfit said:between rounding, truncation and flooring, generally you want to do what the author did when he generated the indexes. Unfortunately, authors don't tell you this. They also don't tell you the remaining decks accuracy that was used during generation. I once looked through all the books trying to figure out what they did, and although it isn't clear, they have used various methods.
I might tend to agree that a TC of +4,(L2) , w/4D's remining, is very close to EV, as a TC of +4, with 2D's remaining, in a 6D game, but in no way do I agree that a TC of +6 in a 6D game, is egual to a TC of +6 in a 2D game at any given point.
Last edited:

